- Zeroing in on any promising results to find their optimal values quickly. When a design space is initially sampled, the values picked rarely result in optimum values. Instead, they produce gradients, that are processed to find optimum locations (usually local maxima/minima) on the response surface. Zeroing in on a locally (but not globally) optimal result requires additional simulation experiments that ultimately don't contribute to finding the global optimum.
- Ensuring that the entire design space is adequately sampled. Consider an egg carton where the peaks and valleys are all slightly different. There are many different local minima and maxima - but only one global value of each. It's easy to find a local gradient and the local peak/valley after initial sampling - but very difficult to ensure that the global value is found. The entire space must be sampled adequately enough that the global maxima/minima have been found by the end of the process.
SHERPA algorithm
Balancing these two different requirements is a difficult task that requires advanced techniques to assess each response as it becomes available to evaluate the numerical order of the response surface and determine the next experiment to run. With most optimizers, this requires considerable understanding of both the problem being solved and the search algorithm itself to "tune" the control parameters for the algorithm.
With HL-DSE, the SHERPA algorithm evaluates responses as the analysis runs and tunes the algorithm automatically. HL-DSE produces a plot of the responses as the analysis proceeds, showing the value(s) obtained from each simulation experiment.
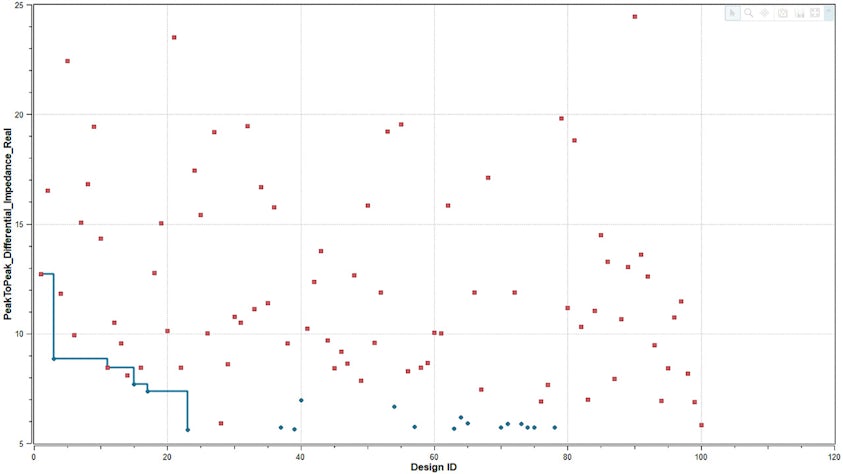
In this plot, HL-DSE has two figures of merit and associated goals:
- optimize red values
- minimize blue values
The blue line shows the history of experiments which improved the value of the blue metric. 100 simulations were given as the budget for this analysis, out of a total of 82,500 possible permutations of input values.
Within 25 simulations SHERPA was able to quickly find near optimal values for each metric.




